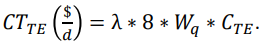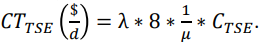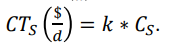INTRODUCCION A LA SIMULACION
Sistemas, Modelos y Simulación
Sistema
- Sistema: Se define como una colección de entidades (por ejemplo, personas, máquinas, etc.) que actúan e interactúan juntas para lograr un fin común. Un sistema está formado por entidades, atributos, actividades, eventos y estado del sistema.
- Entidad: Un objeto de interés dentro del sistema.
- Atributo: Es una característica o propiedad de una entidad.
- Actividad: Es un proceso con determinada duración o proceso que implique cambios con una duración dentro del sistema.
- Evento: Es un inicio o fin de una actividad del sistema.
- Estado del sistema: Es la descripción de las entidades, atributos, actividades según su existencia en algún punto del tiempo. Conjunto de variables necesarias para describir el sistema en un punto particular de tiempo, relativo a los objetivos del estudio.
- Medio ambiente: Todo lo que ocurre fuera del sistema.
- Frontera: Es lo que separa al medio ambiente del sistema.
- Actividad exógena: Actividad que ocurre en el medio ambiente. Ejemplo: proceso de llegada de los clientes al banco.
- Actividad endógena: Actividad que se desarrolla dentro del sistema. Ejemplo: proceso de atención de los clientes en el banco.
- Actividad determinística: Actividad que se conoce de antemano.
- Actividad estocástica: Actividad de la cual no conoce de antemano el tiempo o resultado.
- Sistema discreto: Es aquel en el que las variables de estado cambian instantáneamente en puntos separados en el tiempo.
- Sistema continuo: Es aquel en el que las variables de estado cambian continuamente con respecto al tiempo.
Formas de estudiar un sistema:
- Experimentar sobre el sistema actual vs. experimentar con un modelo del sistema.
- Modelo físico vs. modelo matemático. (condición física vs. relaciones cuantitativas o lógicas)
- Solución Analítica vs. Estudio de Simulación. (método de solución exacta vs. modelo numérico de simulación)
Modelo
- Modelo: Es la representación de un sistema, desarrollado con el propósito de estudiar dicho sistema. Es un cuerpo de información relativa a un sistema con el objetivo de realizar su estudio. Los modelos deben contener sólo los aspectos esenciales del sistema real que representan. Aquellos aspectos del sistema que no contribuyen significativamente en su comportamiento no se deben incluir, ya que lo que haría sería obscurecer las relaciones entre las entradas y las salidas.
- Clasificación: Modelo de Simulación: Matemático / Dinámico / Numérico.
Características de los modelos:
- Deben ser fáciles de entender y manejar
- Deben ser simples y de costo no excesivo
- Deben contar con una buena aproximación del sistema real, que controle el mayor número posible de aspectos del mismo y que éstos contribuyan de forma significativa al sistema (hay relaciones en el sistema que no son significativas y pueden obviarse en el modelo).
Áreas de conocimiento para construir modelos de simulación:
- Modelación: Diseño de modelos matemáticos principalmente.
- Programación: Implementación en un lenguaje de programación.
- Probabilidad y Estadística: Estudiar las variables aleatorias y permitir el diseño y análisis de experimentos.
- Métodos Heurísticos: Llegar a una solución buena del problema planteado.
Simulación
- Simulación:La técnica de resolución de problemas siguiendo en el tiempo los cambios de un modelo de un sistema. Proceso de diseñar un modelo de un sistema real y realizar experimentos con dicho modelo con el propósito de comprender el funcionamiento del sistema o de evaluar diferentes estrategias para la operación del sistema. Proceso de diseñar un modelo matemático o lógico de un sistema real y realizar una serie de experimentos con el ordenador sobre él para describir, explicar y predecir el comportamiento del sistema real.
- Experimentación: Hay dos situaciones que requieren un modelo, cuando la experimentación directa sobre el sistema real es muy costosa o imposible; la otra es la del diseño de un nuevo sistema, así el modelo puede ir modificándose fácilmente hasta obtener el comportamiento deseado.
- Predicción: El modelo se puede usar para predecir el comportamiento del objeto real bajo ciertos estímulos. Se puede hacer así una evaluación de diferentes estrategias de acción.
- Enseñanza y “training”: Se puede utilizar para el adiestramiento de astronautas, en los juegos de negocios, etc.
Proceso de Simulación
- Serie de pasos o “metodología” para llevar a cabo un estudio o proceso de simulación.
- Puede variar en función de diferentes autores o propuestas.
- Se enfoca a estudiar el problema, sus procesos, los datos, construir una modelación del sistema, validarlo, experimentar con él y apoyar la toma de decisiones.
Pasos de un Proceso de Simulación
- FORMULACIÓN DEL PROBLEMA: Se definen las cuestiones para las que se buscan las respuestas, las variables implicadas y las medidas de ejecución que se van a usar.1.Identificación del problema: Se identifica el tipo de problema, los recursos a utilizar, los requisitos, etc.2.Reconocer las variables del sistema: Se identifican las variables del sistema que son de interés, se clasifican en exógenas y endógenas, etc. Se identifican a partir de las actividades o procesos del sistema.3.Especificación de las restricciones de las variables de decisión: Se identifican restricciones del problema planteado. Se tiene muy en cuenta las restricciones sobre las variables de decisión.4.Desarrollar una estructura preliminar del modelo que interrelacione las variables del sistema y las medidas de ejecución: Se definen funciones objetivo que relacione a las variables.5.Desarrollo de un modelo apropiado: Un Modelo es un abstracción de las partes esenciales del sistema. Se verifica si con las variables que se han especificado, se tiene suficiente para describir los aspectos importantes del sistema. Dependerá del propósito del modelo y de la contribución de sus variables.
- COLECCIÓN DE DATOS Y ANÁLISIS: La recogida de datos se ve como el segundo paso, pero es bastante posible que se hayan tenido que recoger datos para formular el problema. En este paso se recoge el mayor volumen de datos, se reduce y se analiza.
Se establece los métodos para la recolección de datos, según cada variable, puede ser manual o utilizando tecnología.
Se toma en cuenta: la capacidad de quien recoja los datos; impacto sobre el sistema real; facilidad de conversión de los datos al ordenador; costo del método de recolección.
Suele ser suficiente la observación directa y recogida manual, pero si la medida que se quiere observar depende de una persona, su comportamiento se puede ver afectado por estar siendo observada. En ocasiones puede que la acción que se quiere observar sea muy rápida y no es factible la observación humana.
Una vez realizado el muestreo, los datos se han de analizar e introducir en el modelo. Los datos usados para definir el modelo pueden ser de dos tipos:1.Determinísticos: Son datos conocidos con certeza. Estos se pueden introducir fácilmente en el modelo2.Probabilísticos: Mediante una distribución de probabilidades.- Usar la muestra de datos recogida para representar la distribución de probabilidades.
- Determinar una distribución probabilística teórica que se comporte como la muestra de datos y usar ésta en el modelo. Esto permite tener una mejor comprensión (generalización) del modelo.
- DESARROLLO DEL MODELO:Incluye la construcción y depuración del modelo del sistema real, incluyendo la selección de un lenguaje de programación y codificación del modelo.
Se divide en dos partes:1.Comprensión del Sistema: Conocer el comportamiento del sistema. Tenemos dos técnicas:- Aproximación de Flujo Físico: Se identifican las entidades cuyo procesamiento o transformación constituye el propósito principal del sistema. Estas entidades pueden tomar diferentes caminos en el sistema, las rutas que siguen se determinan mediante reglas de decisión. La representación del sistema vendrá dada mediante un diagrama de flujo de entidad y los elementos de procesamiento del sistema.
- Aproximación de Cambio de Estado: Verificar el estado del sistema y sus cambios mediante los eventos ocurridos. Se verifican variables. La evolución del sistema se puede representar mediante un grafo de sucesos.
2.Construcción del Modelo: Se realizan algunas tareas principales:- Elección del mecanismo de avance del tiempo. Incrementos fijos de tiempo o en base a eventos. del sistema.
- Si se elige el incremento por eventos, el reloj se inicializa a 0 y se incrementa al siguiente tiempo en que vaya a ocurrir un suceso, en este momento de actualización del reloj se modifican las variables que se vean afectadas por la ocurrencia del suceso.
- Si se elige un incremento de tiempo fijo, el reloj se inicia a 0 y se va actualizando cada vez que pase el incremento de tiempo fijado.
- Elección de un Lenguaje de Programación: Se elije el lenguaje de programación para la implementación del modelo de simulación. Ejemplo: SIMAN.
- Generación de números y variables aleatorias: Se van a necesitar muestras aleatorias para representar valores de variables de entrada probabilísticas.
- Implementación y depuración del modelo: La facilidad o dificultad en esta etapa dependen en gran medida del lenguaje de programación que se haya elegido.
- VERIFICACIÓN Y VALIDACIÓN DEL MODELO: Se dice que un modelo es válido si sus medidas de salida tienen una correspondencia apropiada con las mismas medidas en el sistema real.1.Verificación: Consiste en chequear la consistencia interna del modelo. Se verifica el cumplimiento de restricciones, etc2.Validación: Consiste en asegurar que exista la correspondencia entre el sistema real (realidad) y el modelo. Un buen método para la validación es hacer un test para ver cómo el modelo predice el comportamiento del sistema ante determinadas entradas.
- EXPERIMENTACIÓN Y ANÁLISIS DE LAS SALIDAS:
Se han de diseñar los experimentos que se van a llevar a cabo sobre el modelo y luego analizar las salidas obtenidas, de forma que podamos responder a las cuestiones que se plantearon en la formulación inicial.
El propósito de la experimentación con el modelo es obtener información acerca del comportamiento del sistema, para que esto nos ayude en la toma de decisiones. Cuando consideramos la ejecución de un sistema, se puede desear conocer cómo se comporta dicho sistema en sentido absoluto, o comparativamente, para poder contrastar varias configuraciones alternativas del sistema (experimento).
En la interpretación de las salidas del modelo, hay algunos aspectos que son únicos de la simulación. Mientras que los modelos analíticos proporcionan soluciones con medidas de ejecución completamente definidas, los modelos de simulación producen estimaciones de las medidas que están sujetas a error
Los Resultados son Aproximaciones. Se deben analizar mediante técnicas estadísticas.
Se ha de asegurar que los resultados obtenidos sean aceptados por el usuario.
Se dice que un estudio de simulación apoya a la toma de decisiones. Estas decisiones podrían concluir en la implementación de los resultados.
UNIDAD II. TEORÍA DE COLAS O LÍNEAS DE ESPERA
Teoría de Colas
- La Teoría de Colas es el estudio matemático de las colas o líneas de espera dentro de un sistema. El objetivo de la teoría de colas es modelar sistemas de espera.
- Esta teoría estudia factores como el tiempo de espera medio en las colas o la capacidad de trabajo del sistema sin que llegue a colapsar.
- Dentro de las matemáticas, la teoría de colas se engloba en la investigación de operaciones y es un complemento muy importante a la teoría de sistemas.
- Se trata así de una teoría que encuentra aplicación en una amplia variedad de situaciones como negocios, comercio, industria, ingenierías, transporte y logística o telecomunicaciones.
- Nos permite realizar estudios principalmente de los llamados “sistemas de servicio”.
- La Teoría de Colas, como disciplina matemática, inicia con el trabajo de Agner Krarup Erlang (matemático, estadístico e ingeniero de Dinamarca), quien estudió un modelo de una estación telefónica obteniendo una fórmula para la distribución del número de líneas ocupadas. Erlang publicó el primer artículo sobre la teoría de colas en 1909.
- A partir de este trabajo, la teoría ha sido aplicada en el estudio de un gran número de sistemas de espera como tráfico de aviones, redes eléctricas, sistemas de internet, teoría de inventarios, entre muchos otros.
- Sin embargo, es importante mencionar que mucha de la teoría de hoy en día fue desarrollada sin aplicación práctica sino únicamente por puro interés matemático.
- Es una teoría que ha tenido aportes de varios autores. Existe diversidad de nomenclaturas.
Se han planteado algunos objetivos para la aplicación de la Teoría de Colas:
- Identificar el nivel óptimo de capacidad del sistema.
- Evaluar el impacto que las posibles alternativas de modificación de la capacidad del sistema tendrían (experimentación).
- Establecer un balance equilibrado del sistema.
- Analizar los tiempos de permanencia en el sistema o en la cola de espera.
- Nos permite realizar estudios principalmente de los llamados “sistemas de servicio”.
- En general: Realizar análisis de los sistemas y encontrar alternativas de mejoras, para el cumplimiento de metas u objetivos planteados (costos, tiempos, cantidades, probabilidades). El objetivo principal de analizar estos tipos de sistemas es el de obtener su máximo rendimiento.
Se pueden considerar varios tipos de problemas de gestión relacionados con los sistemas de colas, estos son:
- Problemas de análisis: Se precisa conocer si, dado un sistema, éste está funcionando correctamente (análisis de equilibrio, cumplimiento de alguna condición).
- Problemas de diseño: Se quieren diseñar las características de un sistema que satisfaga un objetivo o meta global (experimentación).
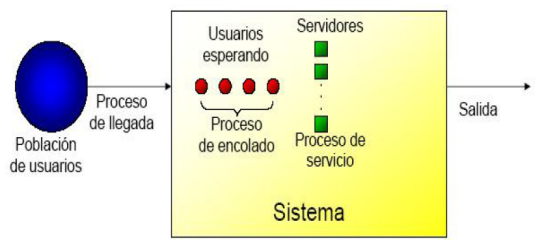
Partes de un Sistema de Colas:
Parámetros:
- M: Tamaño de la población.
- λ (lambda): Tasa a la cual llegan los clientes para ser atendidos. Tasa de llegada.
- µ (mu): Tasa a la cual cada unidad de servicio puede atender al cliente. Tasa de servicio. Representa la máxima capacidad de servicio.
- K: Número de servidores.
- M: Población Infinita / Finita. Muy grande o muy pequeña.
- K: Número de Servidores. Simple (k=1) / Multicanal (k>1).
Recordamos:
Notación de Kendall para el caso de PICS:
Notación: M/M/1
- Tiempos entre llegadas aleatorios con distribución exponencial.
- Tiempos de servicio aleatorios con distribución exponencial.
- K = 1; un único servidor
- Sitio de espera sin restricción.
- M => ∞; Población es INFINITA.

MODELO MATEMÁTICO PICS - M/M/1 - PARÁMETROS DEL MODELO
- M => ∞
- K = 1
- λ (lambda): Tasa a la cual llegan los clientes para ser atendidos. Tasa de llegada. Debe ser conocida.
- µ (mu): Tasa a la cual la unidad de servicio puede atender al cliente. Tasa de servicio. Debe ser conocida.
- CONDICIÓN DE ESTABILIDAD DEL SISTEMA:
λ/μ < 1
MODELO MATEMÁTICO PICS - M/M/1 - FORMULACIÓN MATEMÁTICA
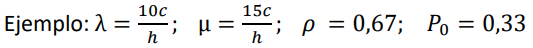
Considerar que:
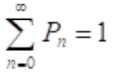
Esta probabilidad nos permite encontrar la probabilidad de que en el sistema se encuentre una cantidad de usuarios, probabilidad de ocurrencia de un evento simple en relación a la cantidad de usuarios dentro del sistema. Considerar que en el sistema pueden estar desde 0 hasta ∞ usuarios, o sea, el sistema puede estar desde vacío hasta máximo toda la población de usuarios en él.

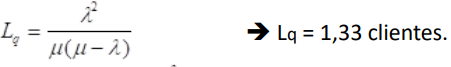
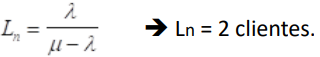
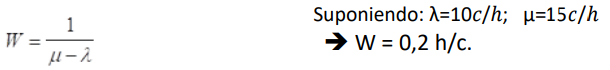

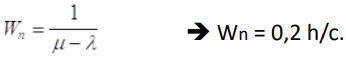
MODELO MATEMÁTICO PICS - M/M/1 - ANÁLISIS ECONÓMICO
- Costo Unitario por Tiempo en Cola (tiempo de espera de los clientes): CTE=> $/h.
- Costo Unitario por Tiempo en el Sistema (tiempo en el sistema de los clientes): CTS => $/h.
- Costo Unitario por Tiempo de Servicio (tiempo en el servicio de los clientes): CTSE => $/h.
- Costo Unitario por el Servidor (alquiler, salario, funcionamiento): CS => $/d.
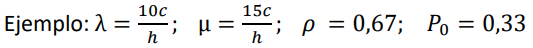
- El costo total sería la sumatoria de los costos individuales de cada concepto.
FÓRMULAS DE COSTOS: Sí: λ => c/ℎ; µ => c/ℎ; 1 día laborable = 8 horas; Costos Unitarios => $/h
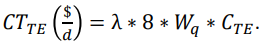

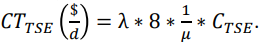
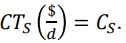

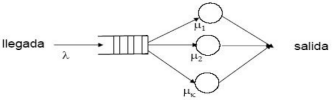
Notación de Kendall para el caso de PICM:
Notación: M/M/K
- Tiempos entre llegadas aleatorios con distribución exponencial.
- Tiempos de servicio aleatorios con distribución exponencial.
- K > 1; un único servidor
- Sitio de espera sin restricción.
- M => ∞; Población es INFINITA.
MODELO MATEMÁTICO PICS - M/M/1 - PARÁMETROS DEL MODELO
- M => ∞
- K > 1; debe ser conocido.
- λ (lambda): Tasa a la cual llegan los clientes para ser atendidos. Tasa de llegada. Debe ser conocida.
- µ (mu): Tasa a la cual la unidad de servicio puede atender al cliente. Tasa de servicio. Debe ser conocida.
- CONDICIÓN DE ESTABILIDAD DEL SISTEMA:
λ/kμ < 1
MODELO MATEMÁTICO PICS - M/M/K - FORMULACIÓN MATEMÁTICA
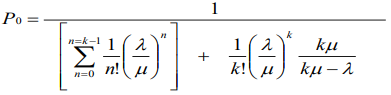
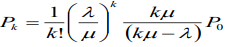
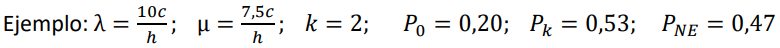
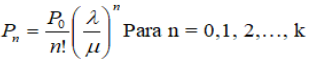
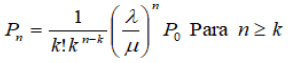
Considerar que:

Esta probabilidad nos permite encontrar la probabilidad de que en el sistema se encuentre una cantidad de usuarios, probabilidad de ocurrencia de un evento simple en relación a la cantidad de usuarios dentro del sistema. Considerar que en el sistema pueden estar desde 0 hasta ∞ usuarios, o sea, el sistema puede estar desde vacío hasta máximo toda la población de usuarios en él.



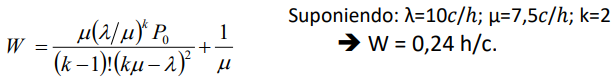

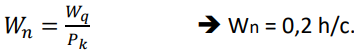
MODELO MATEMÁTICO PICS - M/M/k - ANÁLISIS ECONÓMICO
- Costo Unitario por Tiempo en Cola (tiempo de espera de los clientes): CTE=> $/h.
- Costo Unitario por Tiempo en el Sistema (tiempo en el sistema de los clientes): CTS => $/h.
- Costo Unitario por Tiempo de Servicio (tiempo en el servicio de los clientes): CTSE => $/h.
- Costo Unitario por el Servidor (alquiler, salario, funcionamiento): CS => $/d.
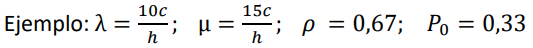
- El costo total sería la sumatoria de los costos individuales de cada concepto.
FÓRMULAS DE COSTOS: Sí: λ => c/ℎ; µ => c/ℎ; 1 día laborable = 8 horas; Costos Unitarios => $/h